|
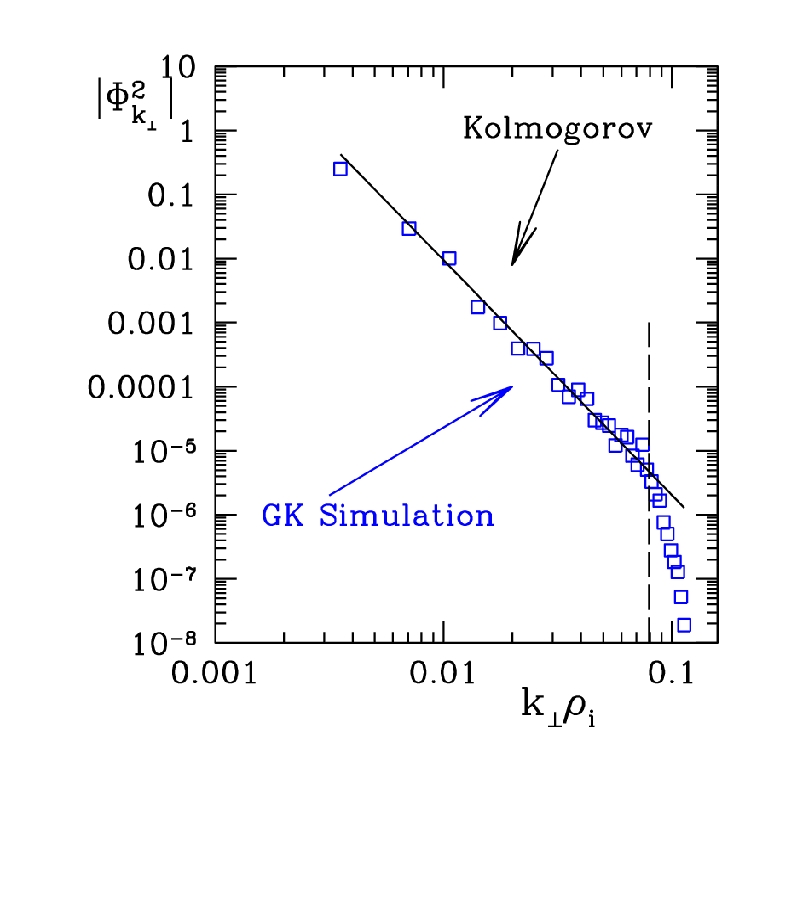
Inertial range spectrum from a GS2 simulation of shear
Alfvén turbulence |
Kinetic Alfvén Wave Turbulence | |
As the turbulent cascade proceeds to smaller
scales, the ideal MHD description of the Alfvén wave is no longer
valid; instead the cascade is made up of kinetic shear Alfvén
waves. The kinetic shear Alv\'en waves (KAW) differ from the shear
Alfvén waves of ideal MHD both linearly (Landau damping) and
nonlinearly (from secondary instabilities, also known as negative eddy
viscosity). The KAW cascade will be simulated using the
electromagnetic gyrokinetic code GS2. A preliminary nonlinear
calculation (above) demonstrates that GS2 correctly describes shear
Alfvén turbulence (i.e., Alfvén turbulence in the MHD regime,
where kinetic effects are irrelevant). This is an important
demonstration of the correct treatment of the nonlinear terms for the
KSA problem. It also provides an independent test of the
Goldreich-Sridhar theory, developed in the MHD regime. [Note that only
the grid resolution changes as one moves from a simulation of MHD to
the KSA regime with a gyrokinetic code.] Here, the plasma was stirred
at the box scale with a forcing function whose amplitude was taken
from a Langevin equation, which in turn was constructed to produce
Alfvén waves with a decorrelation time comparable to the linear wave
period. This approximates the flow of energy into the simulated
scales from larger scales. Hyperviscosity and hyperresistivity were
employed at the small scales, since in this case the scales at which
kinetic damping would occur were not included in the simulation. The
hyper-damping terms become important at the scale of the vertical
dashed line. The expectation from the theory of Goldreich and Sridhar
is that an inertial range should result, with the Kolmogorov spectrum
E ~ kperp-5/3 appearing in the perpendicular
cascade. This corresponds to a slope of
Phi2(kperp) ~ kperp-11/3
which agrees well with the GS2 simulation, as shown in the figure
above.
|
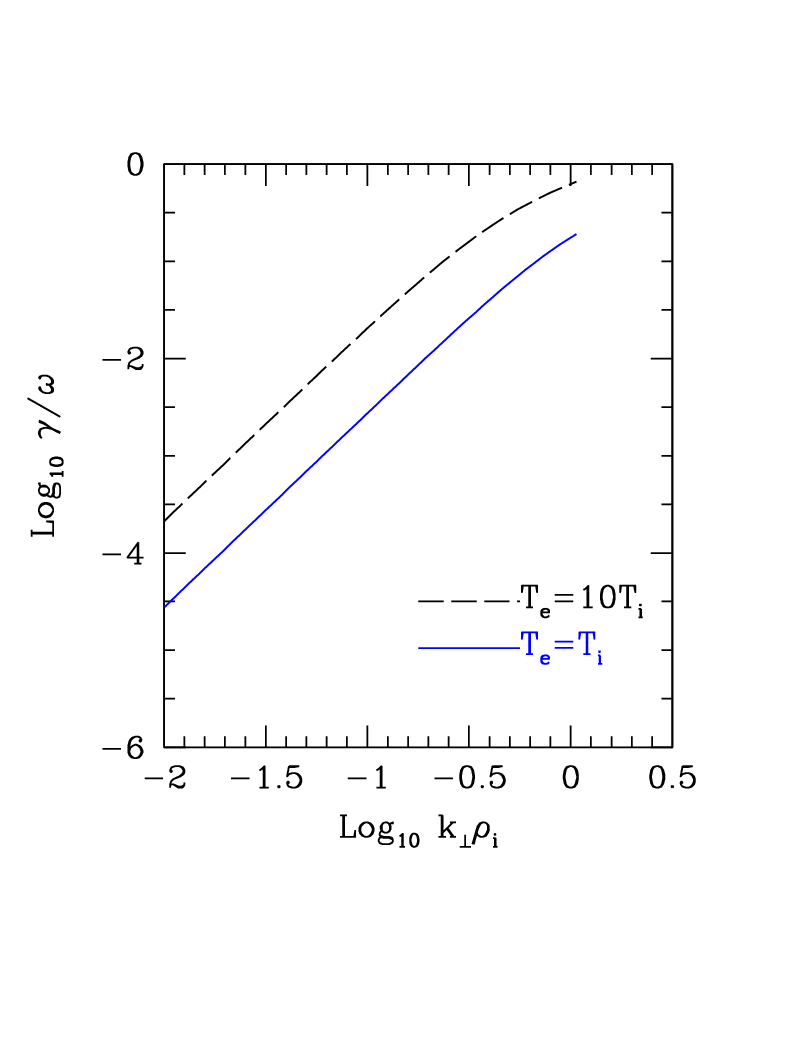
The existing quasilinear theory of kinetic shear Alfvén waves
indicates that much of the energy of the cascade can be drained by
wave-particle interactions as kinetic effects cause the development of
a finite parallel electric field. The associated wave damping for
typical LAPD parameters is shown here. For these LAPD parameters,
the damping is significant, and corresponds mainly to electron
heating.
CMPD supports a comprehensive theoretical and computational investigation
of Alfvén wave cascades. We expect to understand whether the
existing quasilinear estimates of the development of the turbulent
cascade at small scales are qualitatively correct. Other physics may
enter the cascade, such as secondary instabilities or coupling to
other waves. However the cascade develops, one would like to know the
relative heating of ions and electrons. The heating time scale is
long compared to the frequency of small-scale fluctuations. It
remains to be proven that the only interaction between these scales
occurs via the cascade. Such proof may only come from
multiscale computations. Each of these questions requires carefully
designed nonlinear simulations and the development of nonlinear theory
to interpret the results. |
This project should establish that our kinetic simulations of
electromagnetic turbulence (in the form of KAW's) correctly describe
the experimental observations from LAPD. The results will feed
directly into all other research tasks of the Center.
|
|